第一节　衍射衬度的类型及其特点

1.1 TEM中电子显微像的衬度类型

I.振幅衬度

1. 质量厚度衬度 
2. 衍射衬度 
II.相位衬度

3.高分辨像 
质量厚度衬度

质量厚度衬度本质上是一种散射吸收衬度，即衬度是由散射物不同部位对入射电子的散射吸收程度有差异而引起的，它与散射物体不同部位的密度和厚度的差异有关；

衍射衬度

衍射衬度是由于晶体薄膜的不同部位满足布拉格衍射条件的程度有差异而引起的衬度； 
相位衬度

相位衬度是多束干涉成像，当我们让透射束和尽可能多的衍射束，携带它们的振幅和相位信息一起通过样品时，通过与样品的相互作用，就能得到由于相位差而形成的能够反映样品真实结构的衬度（高分辨像）. 

1.2 衍射衬度的来源

衍射衬度是一种振幅衬度，它是电子波在样品下表面强度（振幅）差异的反映，衬度来源主要有以下几种：
1.两个晶粒的取向差异使它们偏离布拉格衍射的程度不同而形成的衬度； 
2.缺陷或应变场的存在，使晶体的局部产生畸变，从而使其布拉格条件改变而形成的衬度； 
3.微区元素的富集或第二相粒子的存在，有可能使其晶面间距发生变化，导致布拉格条件的改变从而形成衬度，还包括第二相由于结构因子的变化而显示衬度； 
4.等厚条纹，完整晶体中随厚度的变化而显示出来的衬度； 
5.等倾条纹，在完整晶体中，由于弯曲程度不同（偏离矢量不同）而引起的衬度. 

1.3 衍射衬度成像的特点

1.衍衬成像是单束、无干涉成像，得到的并不是样品的真实像，但是，衍射衬度像上衬度分布反映了样品出射面各点处成像束的强度分布，它是入射电子波与样品的物质波交互作用后的结果，携带了晶体散射体内部的结构信息，特别是缺陷引起的衬度； 
2.衍衬成像对晶体的不完整性非常敏感； 
3.衍衬成像所显示的材料结构的细节，对取向也是敏感的； 
4.衍衬成像反映的是晶体内部的组织结构特征，而质量厚度衬度反映的基本上是样品的形貌特征。

第二节　衍射衬度的成像方式

2.1 明场像

让透射束通过物镜光阑所成的像就是明场像。成明场像时，我们可以只让透射束通过物镜光阑，而使其它衍射束都被物镜光阑挡住，这样的明场像一般比较暗，但往往会有比较好的衍射衬度；也可以使在成明场像时，除了使透射束通过以外，也可以让部分靠近中间的衍射束也通过光阑，这样得到的明场像背景比较明亮。

a 明场像示意图

2.2 暗场像

仅让衍射束通过物镜光阑参与成像得到的衍衬像称之为暗场像。暗场像又可以分为一般暗场像、中心暗场像和弱束暗场像等。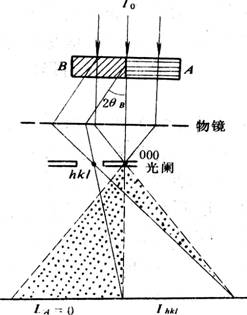

b 普通暗场像示意图

A、一般暗场像

不倾转光路，用物镜光阑直接套住衍射斑所得到的暗场像，就是一般暗场像。

B、中心暗场像

为了消除物镜球差的影响，借助于偏转线圈倾转入射束，使衍射束与光轴平行，然后用物镜光阑套住位于中心的衍射斑所成的的暗场像称之为中心暗场像；中心暗场像能够得到较好的衬度的同时，还能保证图像的分辨率不会因为球差而变差。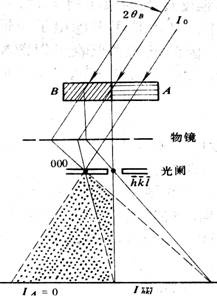 

中心暗场像示意图

C、弱束暗场像

弱束暗场像严格地讲也是属于中心暗场像，所不同的是：中心暗场像是在双光束条件下用g:-g的成像条件成像；而弱束暗场像是在双光束的条件下用g:3g的成像条件成像。

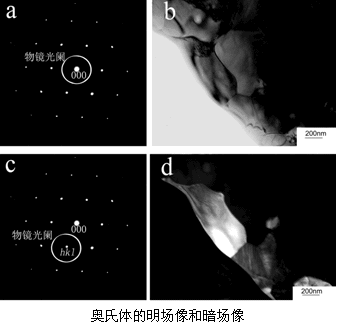
2.3 明暗场像实例 

下图为明场像和普通暗场像的实例。这是在钢铁材料的研究中拍下的奥氏体的明场像和暗场像，其中图a和图c是奥氏体在[011]晶带轴下的电子衍射衍射花样；图b是用物镜光阑直接套住射斑以后成像得到的明场像，图d是在不倾转光路的前提下，直接用物镜光阑套住衍射花样中的一个{200}衍射斑成像得到的普通暗场像，由暗场像可以看出，与衍射花样对应的晶粒应该是变亮的部分。我们看到有两个晶粒同时变亮，表明这两个晶粒的位向应该是比较接近的。另外需要指出来的是，由于在进行明场像和暗场像操作时，并没有特意倾转到双光束条件，因而所得到的明场像和暗场像的衬度并不完全互补。

接下来的图是中心暗场像的实例。它是在研究镁合金中的一种CaMgSi相时通过暗场成像来显示CaMgSi的显微组织特点时得到的显微像。其中图a是CaMgSi析出相的形貌像，图b是与之对应的电子衍射花样，从电子衍射花样可以看出来CaMgSi相中存在二重孪晶，为了显示出二重孪晶的形貌特点，对它进行了中心暗场成像操作。由于电子衍射花样斑点较密，该暗场像也不是在双光束条件下进行的，而是直接将白圈里的斑点用倾转扭移到中心位置，然后后物镜光阑套住该衍射斑成像得到的。图c是与之对应的中心暗场像，从中心暗场像中可以看出来CaMgSi相中实际上存在三个小的孪晶块，不过非常小的那块与右边孪晶的位向完全相同（通过倾转后证实）。中心暗场像的特点是其分辨率由于球差较小所以要好于普通暗场像。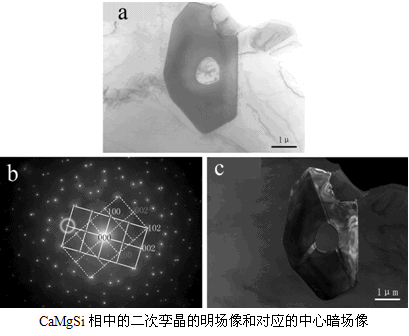

2.4 明场像和暗场像的衬度问题

2.4.1. 双光束条件 

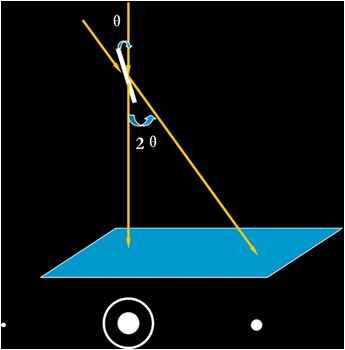
假设电子束穿过样品后，除了透射束以外，只存在一束较强的衍射束精确地符合布拉格条件，而其它的衍射束都大大偏离布拉格条件。作为结果，衍射花样中除了透射斑以外，只有一个衍射斑的强度较大，其它的衍射斑强度基本上可以忽略，这种情况就是所谓的双光束条件。反映在衍射几何条件中就是晶体的倒易点阵中，只有一个倒易阵点与反射球相交，其它的阵点都与反射球相去甚远。由衍射的尺寸效应可知，双光束条件应该在试样较厚的地方比较容易实现。下图即是双光衍射示意图。

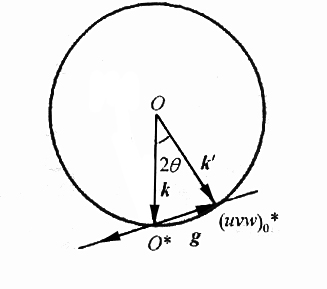
双光束衍射几何示意图

2.4.2. 操作反射 

在用双光束成像时，参与成像的衍射斑除了透射斑以外，只有衍射斑hkl，因此无论是在明场成像还是暗场成像时，如果该衍射斑参与了成像，则图像上的衬度在理论上来讲就与该衍射斑有非常密切的关系，所以我们经常将该衍射斑称为操作反射，记为ghkl.

2.4.3. 明场像的衬度 

假设入射电子束的总的强度为I0, 双光束下成像时，如果透射束的强度和衍射束的强度分别用IT和Id来表示的话，则有： 
Id +IT＝ I0
由上式可以看出，在理想的双光束条件下，明暗场强度是互补的。也就是在明场下亮的衬度，在暗场下应该是暗了，反之亦然。 
需要指出来的是，在非双光束条件下，比如存在多个衍射斑点的情况下，用任意斑点所成的暗场像与明场像显然不会是完全互补的。

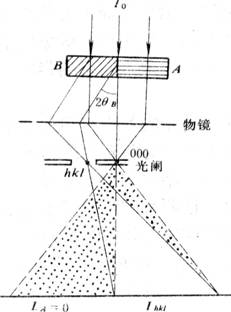
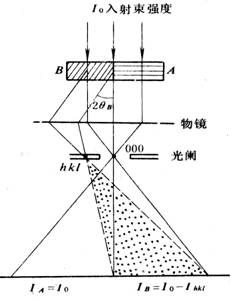
如右图所示，假设样品中A部分完全不满足衍射条件，而样品B只有(hkl)面满足衍射条件（双光束条件）。则在明场下，A部分的像的单位强度为：IA=I0,
而B部分的像的单位强度则为: 
IB＝I0-Ihkl.
以A晶粒的亮度为背景强度，则B晶粒的衬度可以表示为：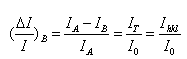
 

2.4.4. 暗场像的衬度

而对于暗场像来讲，双光束条件下A晶粒的强度为0，而B晶粒的强度为Ihkl, 以亮的晶粒B为背景时A晶粒的衬度为：
 
由此可见，暗场成像时的衬度要比明场成像时要好得多。

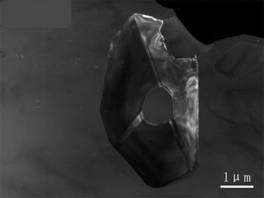
暗场像的衬度实例
a) CaMgSi相中的二重孪晶暗场像; b) CaMgSi相中的三重孪晶暗场.

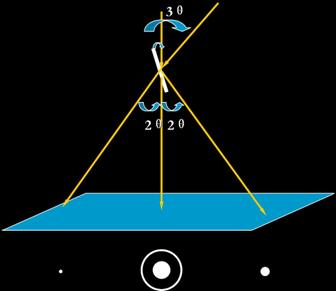
2.4.5. 中心暗场像成像原理与操作

中心暗场的操作要领： 
在双光束条件下将与亮的衍射斑（ghkl）相对的暗衍射斑（g-h-k-l)用倾转旋扭移动到透射斑位置，然后用物镜光阑套住中心位置的斑点成像，得到的就是中心暗场成像。在移动的过程中间，本来暗的衍射斑会越来越亮，而本来亮的衍射斑会越来越暗。这个就是g: (-g)操作。

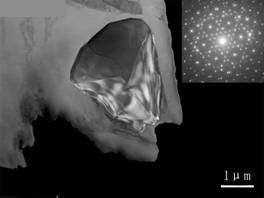
2.4.6. 弱束暗场像成像原理与操作

弱束暗场的操作要领： 
在双光束条件下将亮的衍射斑（ghkl）用倾转旋扭移动到透射斑位置，然后用物镜光阑套住中心位置的斑点成像，得到的就是弱束暗场成像。在移动的过程中间，本来亮的衍射斑会越来越暗。这个就是g: (3g)操作。

弱束暗场像主要用于显示缺陷，比如位错像，无论是在明场还是暗场像下，其背底都会是亮的，也就是说位错的衬度不会太好，但是在弱束暗场像下，位错像是亮的，而背景是暗的，这时位错的衬度会更好。另外在弱束暗场像下，位错像的分辨率会更高。下图是位错像的明场像和弱束暗场像的实例，从图中可以看出在弱束暗场下位错看起来更加清楚。

第三节 衍射衬度的运动学公式的推导

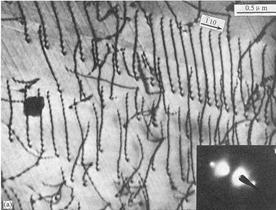
3.1 运动学理论假设

当晶体中存在缺陷或者第二相时，衍射衬度像中会出现和它们对应的衬度，即使是在完整晶体中，也会出现等厚条纹和等倾条纹；晶体中缺陷和衍射衬度之间在尺度和位置上具有怎样的对应性完整晶体中的衬度又是怎样来的？要回答这些问题，必须从理论上来予以解释。要解释清楚TEM下观察到的电子显微像，最理想、也是最直接的方法就是直接算出样品下表面处的电子波分布函数，得出每一点的强度，则无论是衍射衬度还是相衬度都不再成为问题！但是我们知道对于求电子束与样品相互作用后的电子波函数的表达式这样一个实践的问题，根本就不可能解出来。因此，我们必须对问题进行简化。衍射衬度的运动学和动力学理论就是基于这样思想提出的用以解释衍射衬度的两种理论。其中衍射衬度的运动学理论是在以下近似的基础上提出来的：

双束近似
倾转晶体选择合适的晶体位向，使得只有一组晶面(hkl)接近布拉格衍射位置，所有其它晶面都远离各自的衍射位置；

运动学近似
又称为一级Born近似或单散射近似，认为衍射波的振幅远小于入射波的振幅，因而在试样内各处入射电子波振幅和强度都保持不变（常设为单位１），只需计算衍射波的振幅和强度变化；

柱体近似
假设晶体在理论上可以分割成平行于电子波传播方向的一个个小柱体，这些小柱体在衍射过程中相互独立，电子波在小柱体内传播时，不受周围晶柱的影响，即入射到小晶柱内的电子波不会被散射到相邻的晶柱上去，相邻晶柱内的电子波也不会散射到所考虑的晶柱上来，柱体出射面处衍射强度只与所考虑的柱体内的结构内容和衍射强度有关，一个像点对应一个小晶柱下表面；

除了以上近似外，运动学和动力学还涉及到一些近似处理，如：向前散射近似和高压近似等。

3.2 运动学公式的推导

在以上假设的基础上，如果我们能够求出每个小柱体下表面的电子波振幅，则整个像的衬度应该就能表示出来。由于衍射衬度主要用来解释大于1nm的显微组织结构，而我们选取的小晶柱的尺度大约是纳米级，因此我们在求下表面的电子波振幅时可以将整个下表面当成一个点来处理。经过详细地推导后可以得出，如果将每个小晶柱分成无数个小的薄层，则每一个小薄层对下表面的衍射波函数的总的贡献可以表示成： 
 
Ψ0是入射波函数的振幅，在运动学理论中，它总为单位1;
λ：衍射波的波长； 
Fg：晶体单胞的结构因子； 
Vc：晶体单胞的体积； 
θ： 衍射波波矢与水平小薄层之间的夹角。

3.3 消光距离的导出：

引入消光距离这一物理参量实际上已经属于动力学衍射理论范畴了。它是指由于透射束与衍射束之间不可避免地存在动力学交互作用，透射振幅及透射束强度并不是不变的。衍射束和透射束的强度是互相影响的，当衍射束的强度达到最大时，透射束的强度最小。而且动力学理论认为，当电子束达到晶体的某个深度位置时，衍射束的强度会达到最大，此时它透射束的强度为0，衍射束的强度为1.
所谓消光距离，是指衍射束的强度从0逐渐增加到最大，接着又变为0时在晶体中经过的距离。这个距离可以从理论上推导出来。 

上式中，Ψ0是入射束的振幅，取单位1，所以衍射束每穿过一个晶柱的小薄层dz，对P点衍射贡献的振幅就可以写为： 
那么每穿过一个单胞的厚度振幅可以写成： 
可以将上面的振幅值设为常数q。
由上面的结果可以知道，衍射波函数对小晶柱下表面的贡献，每穿过一个单胞的厚度，都可以用dΨg表达出来，每两个单胞厚度之间，振幅是相同的，但相位存在一个很小的差别，那个经过n个单胞厚度以后，电子波函数对下表面总的衍射波振幅的贡献我们可以用振幅相位图表示出来，如下图所示。 

 

上图中，L是经过n个单胞后总的振幅，由前面的动力学讨论，衍射束的强度最大只能等于入射束的强度（1），而上图中衍射束的总的结构振幅最大时是圆的直径，假设衍射波函数经过m个单胞厚度后它对晶柱下表面的贡献值达到最大，也就是说它的总的振幅达到最大，那么此时它应该等于上面圆的直径，由前面的讨论可知，直径的大小应该等于1.由于q的值非常小，每个q值接近等于上图中对应的圆弧，因此有：mq=π*1/2（半径）。代入q的值马上可以得到m的值，所以消光距离就等于2m个单胞的长度，所以消光距离可以表示成： 
 

3.4 衍射衬度运动学理论推导过程中存在的问题： 
 
上式中，其相位因子(Kg-K0).r一般表示两束波的程差，很容易让人误以为衍衬成像是一个干涉成像过程，但事实并非如此，衍衬成像是一个非相干的单束成像过程；在衍衬运动学的推导过程中，f和Fg都是表示单位体积的散射因子（结构因子），实际上暗示着薄层中每一处的散射因子都是相同的，这与事实是不相符的，实际上晶体中只有有原子的地方才有散射； 在衍衬运动学的推导过程当中，实际上是假设右图中小晶柱中的小薄层的面积是无穷大的，因为只有这样，这一薄层对P点的总的散射振幅贡献才能等于第一半波带的一半，这一假设显然是不合理的； 在衍衬运动学理论的推导过程中，实际上是把小晶柱的下表面当成一个点P来处理的，看起来很不合理，但考虑到衍衬成像的分辨率极限是1.5nm，而小晶柱的尺度在1nm以内，因而这样处理还是可以的.

第四节 完整晶体的衍衬运动学分析

4.1 完整晶体的衍衬运动学公式推导

由电子衍射的几何关系有：Kg-K0=g+s,因此小晶柱里每个薄层对下表面的散射贡献又可以表示成：

对于完整晶体而言，每个薄层的厚度可以取成一个单胞的厚度，而位置矢r的位置可以取在单胞的平移矢处，这时有g.r=整数，这时上式等于：

为了积分出整个晶柱对下表面的散射贡献，先将s和r写成标量的形式，由图可知，s总是平行小晶柱，并指向下，所以一般取正值（为了积分方便，一般取向下为正）；对于r来讲，由于它是由P点指向小薄层的位矢，方向向上，所以一般取负值，又因为r与厚度方向基本平行，可以将其写成-z；这时的散射波函数公式可写为： 
 
对整个小晶柱积分，最柱体下表面处总的散射波函数为：

 积分后得到：

因此理想晶体中，电子波与小晶柱相互作用后，对下表面总的散射强度可以表示为： 
 

4.2 等厚条纹产生的原理

将上式稍微变形可以得到： 

由上式可知，在理想晶体中，当偏离矢量为常数时，电子衍射衬度的强度随厚度t而变化，这就是等厚条件产生的理论依据。由上式我们可以得到等厚条纹应该具有如下特点：
等厚条纹是当偏离矢量为恒定值时，衍射强度随传播深度的变化而按余弦函数周期的变化，在衬度像上观察到的明暗相间的条纹，同一条纹对应的厚度是相同的，条纹的深度周期为 1/s ； 
衍衬像中的等厚条纹与可见光中的等厚干涉条纹的形成原理是完全不同的；可见光中的等厚干涉条纹是由楔形样品的上下表面的反射波互相干涉而形成的，其衬度来自于两束波的相位差角，而电子衍衬像中的等厚条纹则是单束、无干涉成像，其衬度来自于衍射波的振幅；

等厚条件形成的示意图及实例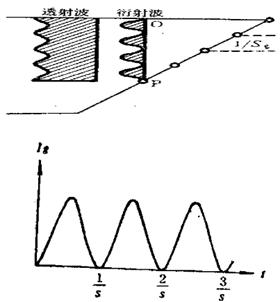 
 

等厚条件形成的示意图

 
等厚条纹明场像 等厚条纹暗场像

4.3 等倾条纹产生的原理 

当衍衬成像时，如果试样的厚度基本不变，而晶体的取向由于变形等原因而有微小的变化时，相当于偏离矢量s有微小的变化，这时衍射波对小晶柱下表面的强度贡献公式可写为： 
 

这时电子衍射衬度的表达式是偏离矢量的函数，随着偏离矢量的改变，衬度改变，这是等倾条纹产生的原因。由上面的表达式可以知道，等倾条纹具有如下的特点：
试样下表面处的强度将随偏离参量 s变化而呈单缝衍射函数的形式变化，衍射强度在s=0处有强度的主极大主极大的半宽高为1/t ，在s=n/2t 中，当n为奇数时，分别对应次极大、三极大等等，当n为偶数时，强度值将为零；
等倾条纹的形成示意图及实例：

第五节 非完整晶体的衍衬运动学分析

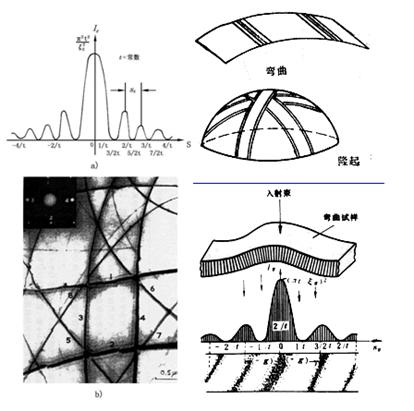
5.1 非完整晶体的衍衬运动学公式推导

对于非完整晶体，描述散射元位置的矢量为：r′=r+R
因此整个畸变后的晶柱对下表面的散射贡献为： 
 
上式中，g.r =整数，s.R是一个无穷小项，因此畸变后的晶柱对下表面的散射贡献最终为： 
 

缺陷的存在引进了一个附加相位因子项2π g.R ，正是由于有相位因子项的存在，使得不同的缺陷会具有不同特点的衬度。

5.2 层错引起的衬度

所谓层错是指晶体中具有某种堆垛次序的原子面，由于错排而引入的缺陷；
层错总是发生在密排的晶体学平面上，层错面两侧分别是位向相同的两块理想晶体，它们之间相互错动了位移矢 R ；
对于面心立方晶体的 {111}层错，R可以是±1/3〈111〉或者± 1/6〈112〉，它们分别代表着层错生成的两种机制。
层错是晶体缺陷中最简单的平面缺陷，其位移矢是一个恒定的值，因而由其产生的相位差角 2π g.R 将为一恒定的值，当g.R为一整数时，由上式可知，积分号后的第一项将为1，层错引起的衬度将不存在，层错将不可见。

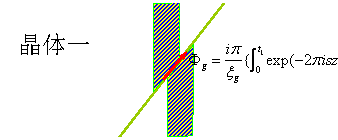
对于层错而言，晶体一和晶体二具有完全相同的位向，它们之间仅仅是在层错面上相差一个滑移矢，在有层错的区域任选一个小晶柱，设该小晶柱中，层错在深度t1处，则整个小晶柱对下表面散射波振幅的总的贡献为：
 

积分之后得：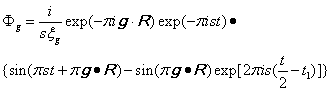 
 
与之对应的强度表达式为：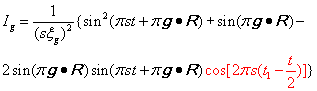
 

由上式可以看出，当偏离矢量为常数时，如果层错可见（g.R不为整数），则小晶柱下表面的电子衍射波强度，只取决于层错所在位置样品的厚度，也就是说层错的衬度是样品厚度的函数。有鉴于此，层错的衬度应该具有如下的特点：
对于确定的层错，当操作反射确定时，则 g.R确定，在样品厚度t和偏离矢量s都确定的前提下，Ig将随层错所在位置的深度t1周期变化，周期为1/s ，与层错的类型无关，其周期函数与等厚条纹一样，都是余弦函数；
当层错在样品中的深度相同时，会具有相同的强度，故层错的衍衬象表现为一组平行于样品表面和层错交线的明暗相间的条纹； 
当衍射矢量偏离布拉格位置的程度增加时， s增大，层错条纹间的间距变小（条纹变密），层错的衍衬强度锐减；
由层错强度的周期函数特点， cos[2πs(t1－t/2)]，可知层错条纹的强度总是中心对称的，（这一点才是层错条纹区别于等厚条纹的最本质特点）；
由周期函数特点可知，当层错面平行样品表面时将不显示衬度。 
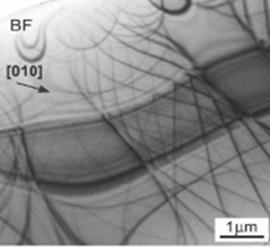
层错衍衬像示意图及实例 
 

层错像实例

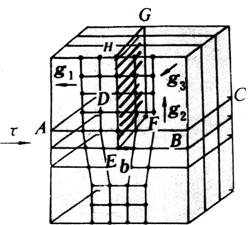
5.3 螺型位错引起的衬度 

螺型位错的几何模型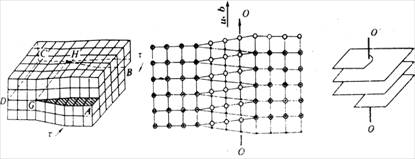 


 

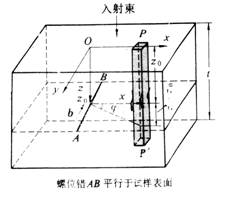
由上图可知，由于螺位错的存在而引入的位移矢可以表示成：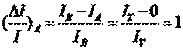 
 

其中z是小晶柱中薄层所在的位置，而z0是位错距样品表面的距离，而x则是位错到小晶柱的距离。
因此由于螺位错的存在而引起的相位差角的变化可以表示成：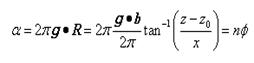 
 

其中α是由于螺位错的位移矢引起的相位角改变；n=g.b 
在位错附近处某一小晶柱对其下表面处的总的衍射贡献为：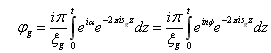 
 

由上面的表达式可以看出来，要使由于螺位错的存在而引入的附加项的值为1，则n必须等于0，即g.b=0时，才不会出现衬度，因此g.b=0是螺位错不可见的判据。

5.4 刃型位错和混合型位错引起的衬度 

刃型位错的几何模型 

 

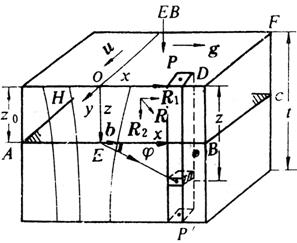
刃位错的应变场可以写为：R=R1+R2。应变场可以表示为：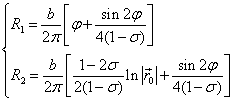 
 

其中其中R1平行于柏式矢量，R2垂直于位错所在的滑移面，σ为泊淞比，φ是从柏式矢量到散射元的极角，r0是柱体内散射元关于位错核心的径向座标.
混合型位错的应变场矢量可以写成：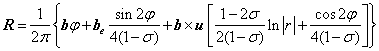 
 

将这些应变场引起的位移矢代入公式： 
 

会得到一个附加位向因子非常复杂的表达式，经过详细分析后可以得出，刃位错和混合位错有如下特点： 
刃位错和混合位错不可见判据是： g.b ＝0且同时要
g.（b * u)＝0；但是由于g.b ＝0时，即使另外一项不为零，其衬度也会非常低，因此实际上对于所有的位错，都采用g.b ＝0作为不可见判据。

5.5 位错衬度像偏离真实位置的解释

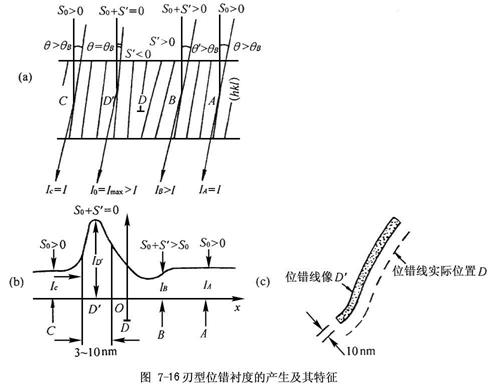
5.6 位错像的特点： 

如上图所示，当衍射条件使基体偏离布拉格条件时（存在偏离矢量时），刃位错中多余半原子面的位向应该与基体相同，因而它并不满足布拉格条件。而在位错的应变场中，有一个相当宽的范围内，晶面接近满足布拉格条件，接近产生衍射带。因此在明场像下，这一个宽的衍射带实际上就是我们看到的暗的位错线。因此这样的位错线往往看起来是很粗的，大约有80~120埃。另外，位错像距离位错的真实位置也会比较远，大约在80~100埃。 
用弱束暗场的方法可以使位错的分辨率提高，而且可以使其像与真实位置更加接近。这是因为弱束暗场是在大的偏离矢量下成像，在大的偏离矢量下，只有畸变量大的晶面才能接近满足布拉格条件，我们知道只有在靠近位错的地方，才存在大的畸变区，因此在弱束暗场下，只有在靠近位错线的很近部分才能显示衬度，而且这个宽度也会比较小。在弱束暗场下位错线的分辨率可以达到 15埃，位错像距位错的真实位置的距离大约为20埃。 
这是从衍射几何来解释位错像的形成原因。当从理论上来分析时，根据动力学原理，位错线的宽度约为有效消光距离 ξgeff的1/2~1/5。而有效消光距离可以表示成：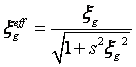

由上式可以看出，在大偏离矢量下（弱束暗场），位错线像的宽度要窄得多。

5.7 位错衬度像实例

NiAl合金中的位错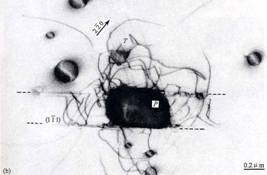
 

不锈钢中析出相周围的位错缠结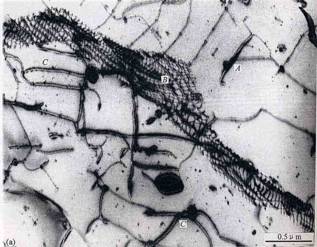

 

 位错缠结形成的晶界

 

 超塑性变形Al-40wt%Zn合金中的小角晶界处的位错形态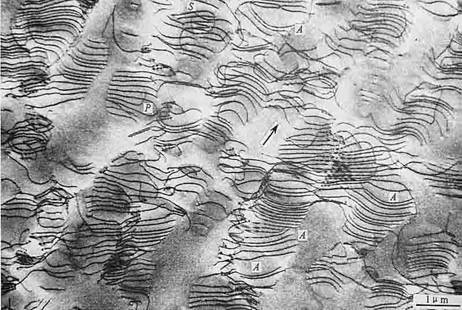

 

Ni基高温合金高温蠕变后的位错组态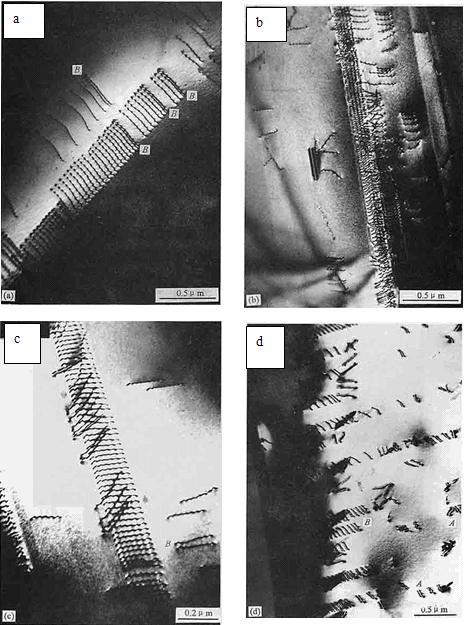

 
Ni基高温合金经固溶处理和形变后的位错组态 
(a) 未变形；(b) 200oC, 形变2%
(c) 200oC, 形变2%； 
(d)-196oC, 形变2%

5.8 第二相粒子形成的衬度 

由于第二相粒子的存在而引入的衬度主要有以下几种：

基体周围应变场引起的衬度；
第二相与基体由于位向差引起的衬度； 
结构因子差别而形成的衬度； 
特定情况下形成的波纹图； 
第二相和基体存在的相界面引起的衬度；

上面的内容中，波纹图在电子衍射部分已经介绍过，结构因子差别而形成的衬度可以当成等厚条纹的问题来处理，相界面引起的衬度其实与层错类似（层错就是其中的一种），但要复杂得多。 
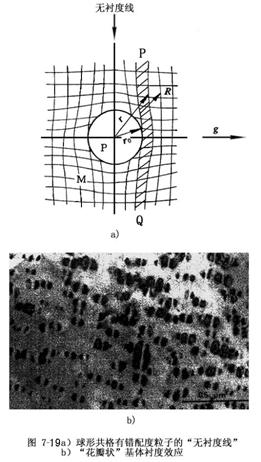
这一部分我们主要来讨论球形第二相粒子导致的应变场衬度。 
对于球形粒子引起的位移矢，在球的外部，可以表示为：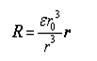 
 
在球的内部，可以表示为：R=－εr. 
由畸变后的晶柱对下表面的散射贡献表达式： 
 

考虑到球形第二相粒子的应变场位移矢的特点，它是中心对称的，因此其衍射衬度具有自身的特点： 
第二相粒子衬度消失的判据严格地讲也是 g.R＝整数，但由于球形粒子中任意方向都存在应变矢量，所以这个判据只能判断一些数学上的点消光，实际上我们能够看到的衬度是当某个面上的应变场矢量都垂直于g时，这个面上的所有衬度都不可见，这时g.R ＝0，因此我们认为第二相粒子的衬度消失的判据为g.R ＝0；另外，由于应变场是球形对称的分布的，所以对于任意操作反射，与之平行的平面上的任意位移矢都能使g.R ＝0，因此，当改变操作反射时，第二相质点衍衬像上的“无衬度线”也将随之改变，但该线将始终与操作反射矢量垂直。

第二相粒子衍射衬度及无衬度线实例

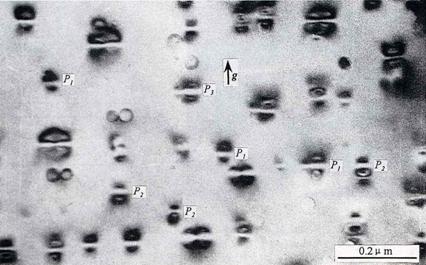
奥氏体不锈钢中的共格应变含铜沉淀相

5.9 运动学理论的不足之处 

等倾条纹的衬度表达式为:

上式中，当s趋向于0时，衍射波的强度趋向于π2t2/ξ2，即当样品的厚度大于ξ/π时，衍射波的强度要大于1，在入射波强度等于1的前提下，衍射波的强度能够大于1，这显然是不合理的；
2、在解释等厚条纹时，产生等厚条纹的深度周期为Δt=1/s ,所以当s→ 0时， Δt将为无穷大，也就是说，在接近双光束成像时，将不可能看到等厚条纹，这与事实完全不符；

第六节 衍射衬度的动力学理论

衍衬动力学理论是在运动学理论的基础上发展起来的，它的主要特点是在散射过程中考虑电子波在晶体中的多次散射问题，即考虑透射束与衍射束之间以及衍射束与衍射束之间的交互作用；也就是说，运动学中的运动学近似已不再成立，但除此之外，运动学理论中的其它假设如双束近似、柱体近似、向前散射近似和高压近似等仍然成立。 
在双束条件下，沿一个小晶柱传播的电子波函数可写成： 
 
如果波函数满足动力学条件，则对于完整晶体，应满足：

 

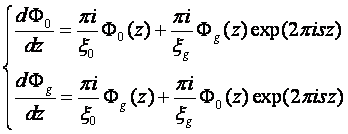
上述方程组与定态薛定谔方程相比，虽然要简单，但要直接求解依然不可能，为此，引入下列两个中间函数：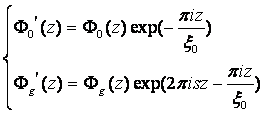 

 

方程组两边同时求导后，代入和后，会发现Φ0(z)和Φg(z)是可求解的。最终的结果是：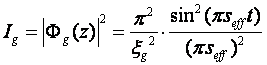 
 

其中：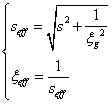
Seff为有效偏离矢量，而ξeff为有效消光距离；

由上面的衍射强度表达式可以看出，即使在严格的双光束条件下，s=0时，有效偏离矢量seff的值也不会为零，此时等厚条纹的深度周期Δt=1/seff，也就是该衍射矢量的有效消光距离； 
另外，对于等倾条纹而言，当 s=0时，，其值也是总是小于1的。因此用衍射衬度的动力学理论来解释晶体中的衍射衬度像将更加合理。

总结

1. 衍衬成像是单束、无干涉成像，得到的并不是样品的真实像，但是，衍射衬度像上衬度分布反映了样品出射面各点处成像束的强度分布，它是入射电子波与样品的物质波交互作用后的结果，携带了晶体散射体内部的结构信息，特别是缺陷引起的衬度；
2. 运动学理论是在运动学近似、双束近似以及柱体近似等近似的前提下通过计算形成的理论，运动学理论对于一般衍衬像的解释是合理的，但是在某些特殊情况下理论与实际有较大差距；
3. 动力学理论是在运动学理论的基础上发展起来的，它进一步考虑了入射束与衍射束之间的交互作用以及多次衍射对衍射衬度的影响，对衍射衬度像的解释更加合理。