第一章 X射线基础(续)
1.6 晶体对X射线的衍射
X射线照射到晶体上发生散射,其中衍射现象是X射线被晶体散射的一种特殊表现。晶体的基本特征是其微观结构(原子、分子或离子的排列)具有周期性,当X射线被散射时,散射波中与入射波波长相同的相干散射波,会互相干涉,在一些特定的方向上互相加强,产生衍射线。晶体可能产生衍射的方向决定于晶体微观结构的类型(晶胞类型)及其基本尺寸(晶面间距,晶胞参数等);而衍射强度决定于晶体中各组成原子的元素种类及其分布排列的坐标。晶体衍射方法是目前研究晶体结构最有力的方法
1.6.1 衍射几何方程
联系X射线衍射方向与晶体结构之间关系的方程有两个:劳埃(Laue)方程和布拉格(Bragg)方程。前者基于直线点阵,而后者基于平面点阵,这两个方程实际上是等效的。
.1 劳埃(Laue)方程
首先考虑一行周期为a0的原子列对入射X射线的衍射。如图1.10所示(忽略原子的大小),当入射角为α0时,在αh角处观测散射线的叠加强度。相距为a0的两个原子散射的X射线光程差为a0(cosαh - cosα0),当光程差为零或等于波长的整数倍时,散射波的波峰和波谷分别互相叠加而强度达到极大值。光程差为零时,干涉最强,此时入射角a0等于出射角,衍射称为零级衍射。
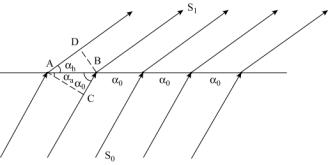
图1.10 一行原子列对X射线的衍射
晶体结构是一种三维的周期结构,设有三行不共面的原子列,其周期大小分别为a0、b0、c0,入射X射线同它们的交角分别为α0、β0、γ0,当衍射角分别为αh、βk、γl,则必定满足下列的条件:
a0(cosαh - cosα0)=
hλ
b0(cosβk - cosβ0)=
kλ
(1.13)
c0(cosγl - cosγ0)= lλ
式中h,k,l为整数(可为零和正或负的数),称为衍射指标,λ为入射线的波长。式(1.13)是晶体产生X射线衍射的条件,称劳埃方程。衍射指标hkl的整数性决定了晶体衍射方向的分立性,每一套衍射指标规定了一个衍射方向。
.2 布拉格方程
晶体的空间点阵可划分为一族平行且等间距的平面点阵(hkl),或者称晶面。同一晶体不同指标的晶面在空间的取向不同,晶面间距d(hkl)也不同。设有一组晶面,间距为d(hkl),一束平行X射线射到该晶面族上,入射角为θ。对于每一个晶面散射波的最大干涉强度的条件应该是:入射角和散射角的大小相等,且入射线、散射线和平面法线三者在同一平面内(类似镜面对可见光的反射条件),如图1.11a所示,因为在此条件下光程都是一样的,图中入射线s0在P,Q,R处的相位相同,而散射线s在P’,Q’,R’处仍是同相,这是产生衍射的必要条件。
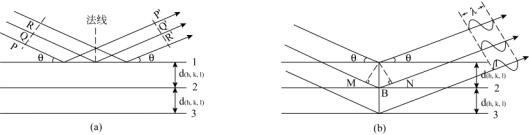
图1.11 布拉格方程的推引
现在考虑相邻晶面产生衍射的条件。如图1.11b所示的晶面1,2,3,…… 间距为d(hkl),相邻两个晶面上的入射线和散射线的光程差为:MB+BN,而MB=BN=d(hkl) sinθn,即光程差为 2d (hkl) sinθn,当光程差为波长λ的整数倍时,相干散射波就能互相加强从而产生衍射。由此得晶面族产生衍射的条件为:
2 d (hkl) sinθn= nλ
(1.14)
式中n为1,2,3,……等整数,θn为相应某一n值的衍射角,n则称衍射级数。式(1.14)称为布拉格方程,是晶体学中最基本的方程之一。
根据布拉格方程,我们可以把晶体对X射线的衍射看作为“反射”,并乐于借用普通光学中“反射”这个术语,因为晶面产生衍射时,入射线、衍射线和晶面法线的关系符合镜面对可见光的反射定律。但是,这种“反射”并不是任意入射角都能产生的,只有符合布拉格方程的条件才能发生,故又常称为“选择反射”。据此,每当我们观测到一束衍射线,就能立即想象出产生这个衍射的晶面族的取向,并且由衍射角θn便可依据布拉格方程计算出这组平行晶面的间距(当实验波长也是已知时)。
由布拉格方程,我们可以知道如果要进行晶体衍射实验,其必要条件是:所用X射线的波长λ< 2d。但是λ不能太小,否则衍射角也会很小,衍射线将集中在出射光路附近的很小的角度范围内,观测就无法进行。晶面间距一般在10埃以内,此外考虑到在空气中波长大于2埃的X射线衰减很严重,所以在晶体衍射工作中常用的X射线波长范围是0.5至2埃。对于一组晶面hkl,它可能产生的衍射数目n决定于晶面间距d,因为必须满足nλ< 2d。如果我们把第n级衍射视为和晶面族hkl平行但间距为d/n的晶面的第一级衍射(依照晶面指数的定义,这些假想晶面的指数为nh,nk,nl,在n个这样的假想晶面中只有一个是实际晶体结构的一个点阵平面),于是布拉格方程可以简化表达为:
2 d sinθ =λ
(d = d/n)
(1.15)
因为在一般情况下,一个三维晶体对一束平行而单色的入射X射线是不会使之发生衍射的,如果要产生衍射,则至少要求有一组晶面的取向恰好能满足布拉格方程,所以对于单晶的衍射实验,一般采用以下两种方法:1.用一束平行的“白色”X射线照射一颗静止的单晶,这样,对于任何一组晶面总有一个可能的波长能够满足布拉格方程;2.用一束平行的单色X射线照射一颗不断旋转的晶体,在晶体旋转的过程中各个取向的晶面都有机会通过满足布拉格方程的位置,此时晶面与入射X射线所成的角度就是衍射角。对于无织构的多晶样品(如微晶的聚晶体,很细的粉末等),当使用单色的X射线作入射光时,总是能够产生衍射的。因为在样品中,晶粒的取向是机遇的,所以任意一种取向的晶面总是有可能在某几颗取向恰当的晶粒中处于能产生衍射的位置,这就是目前大多数多晶衍射实验所采用的方法,称为“角度色散”型方法。对于多晶样品采用“白色”X射线照射,在固定的角度位置上观测,则只有某些波长的X射线能产生衍射极大,依据此时的角度大小和产生衍射的X射线波长就能计算得出相应的晶面间距大小,这就是所谓“能量色散”型的多晶X射线衍射方法。
1.6.2 多晶X射线的衍射强度
劳埃(Laue)方程和布拉格(Bragg)方程只是确定了衍射方向与晶体结构基本周期的关系,通过对衍射方向的测量,理论上我们可以确定晶体结构的对称类型和晶胞参数。而X射线对于晶体的衍射强度则决定于晶体中原子的元素种类及其排列分布的位置,此外,还与诸多其它的因素有关。
所谓衍射强度是指“积分强度”,积分强度是一个能量的概念,一个在理论上能够计算并且实验上也能测量的量。在晶体衍射的记录图中(照片、照片的光度计扫描图或衍射仪记录图等),照片的黑度或衍射仪记录图的强度曲线下面的面积,应该与检测点处的衍射线功率成正比,比例系数是仪器条件的函数。在理论上以检测点处通过单位截面积上衍射线的功率定义为某衍射线的强度(绝对积分强度)。纯物质衍射线强度的表达式很复杂,但是可以简明地写成下面的形式:
I = I0·K·|F|2
(1.16)
式中:I0为单位截面积上入射的单色X射线功率;|F|称为结构因子,取决于晶体的结构以及晶体所含原子的性质。结构因子可由下式求算:
Fhkl = ∑ fn·exp[2πi(h xn + k yn +l zn)]
(1.17)
式中fn是晶体单胞中第n个原子的散射因子,(xn、yn、zn)是第n个原子的坐标,h、k、l是所观测的衍射线的衍射指标,公式求和计算时需包括晶体单胞内所有原子;K是一个综合因子,它与实验时的衍射几何条件,试样的形状、吸收性质,温度以及一些物理常数有关。对于粉末衍射仪而言(粉末衍射仪使用时将样品压成平板状,入射线和衍射线对样品平面的交角总是相等的),K由下式求算:
![]() (1.18)
(1.18)
① ② ③ ④ ⑤ ⑥ ⑦
式中:
因子①与实验条件有关:A为样品受照射的面积,R为衍射仪圆的扫描半径;
因子②是一些物理常数:e为电子的电荷,m为电子的质量,C为光速,λ为实验时X射线的波长;
因子③称作多重性因子,在粉末衍射中,晶面间距相等的晶面其衍射角相等,由于对称性的联系,这些晶面可能有j种晶面指标;
因子④中V是单位晶胞的体积;
因子⑤是衍射仪条件下的洛伦茨偏振因子;
因子⑥为温度因子,原子的热振动将使衍射减弱,故衍射强度与温度有关;
因子⑦ 是衍射仪条件下的吸收因子,它只和样品的吸收性质有关。